 【 微信扫码咨询 】
【 微信扫码咨询 】

六自由度平台的运动学和动力学是各国学者竞相研究的两大领域。并联机构动力学的问题十分复杂,导致取得的相关理论成果较少。研究六自由度平台各支腿力矩与负载平台的关系,就必须对其建立动力学模型。
数学建模是研究空间问题常用的方法之一,通过建立模型可以对抽象的问题作定量的分析,方便研究。运用Newton-Eulr法建立了六自由度平台的动力学模型,并应用Matlab编写动力学力矩算法并进行仿真,对六自由度平台的动力学进行了具体的分析。
牛顿-欧拉动力学方程
我们假设六自由度平台的每个部件都为刚体,只有给刚体一个加速度或减速度才能使刚体运动,但产生加速度就必须给刚体相应的力,而这个力又是关于加速度和刚体质量分布的函数,也就是有一个在一定条件下可以相互转换的关系。为了得出它们之间的函数关系,可以利用牛顿方程和欧拉公式,经过推导即可得出平台各支腿驱动力矩、负载力、惯量和加速度之间的关系。
在利用牛顿方程和欧拉公式进行动力学方程推导前,我们先分析下转动惯量的计算。转动惯量的定义是刚体在转动时候会产生一个惯性,把这个惯性作一个定量的表示。转动惯量在后边求取六自由度平台支腿角速度,角加速度和力矩时都会用到。
如下图所示,可以得到刚体在坐标系 下的惯量矩阵为:
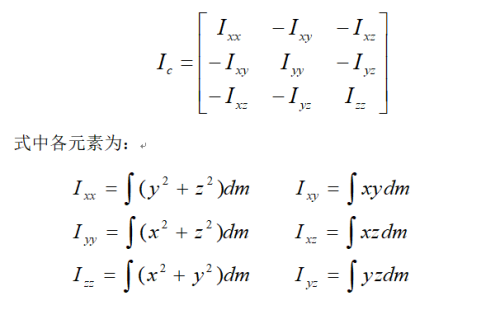
由于在下面动力学方程的推导过程中也会用到平行轴定理,在这里就简单的介绍一下。首先在上面得出了刚体于坐标系下的惯量张量,平行轴定理指的是计算坐标系平移时刚体惯性张量的方法。下面给出坐标平移后相对于坐标系{A}的惯性张量为:
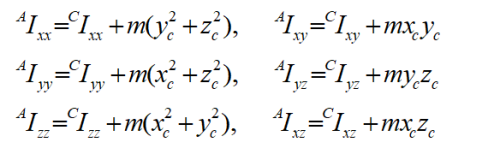
以上是对六自由度平台刚体质量分布做的简单的分析,给出了惯性矩阵方程以及平行轴定理的表达式。基于这些前期工作的准备,下面对牛顿—欧拉方程进行阐述。首先对质心的平动进行研究,如上图所示, 表示质心处的位置,那么质心处的加速度为 ;在绕质心的转动分析过程中,假设刚体转动的角速度,则令表示角加速度,则可以得出作用在刚体质心 处的力和力矩方程为:
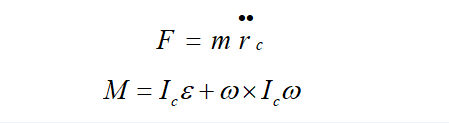
 网站二维码
网站二维码
 微信二维码
微信二维码
网站地图 苏州通诺尔智能科技有限公司 版权所有 2008-2021 苏ICP备2021049911号